Champ électrique rayonné par une antenne
Champ électrique rayonné par une antenne
Pour quelle raison c’est parfois 5/d ou parfois 7/d ?
Cette question relative au calcul de l’intensité de champ électrique d’une antenne est fréquemment posée dans pléthore de forums topiques. Les réponses qui y sont données manquent, à mon avis, de consistance. J’espère que ma réponse sera à même de combler cette lacune.
Calcul du champ électrique d’un dipôle (en V/m).
Préambule
E se calcule à partir de la formule suivante:
E2 = W x R (comme dans la loi connue…P= U2/R), avec :
E = champ électrique en volts par mètre
W = puissance rayonnée par unité de surface (watts par mètre carré) à la distance r de l’antenne en mètres
R = impédance du milieu de propagation en ohms
Impédance du milieu de propagation.
C’est le rapport entre le champ E en volts par mètres et le champ H en ampères par mètres. En divisant des volts par des ampères, on obtient des ohms.
A partir des lois de l’électromagnétisme, nous avons les relations suivantes :
E = v.B,
B est l’induction magnétique,
v est la vitesse de propagation, soit 3.108m/s dans l’air.
H = B / µ0 .µr
µ0 = 4pi.10-7 est la perméabilité magnétique du vide
µr = 1 est la perméabilité magnétique relative de l’air
https://pastel.archives-ouvertes.fr/tel-01316557/document
http://www.electronique-et-informatique.fr/Electronique-et-Informatique/Electromagnetisme.php
Ainsi Z = E / H, soit :
![]()
Soit les 377 ohms de l’impédance intrinsèque du vide notée Z0 ou Zc.
https://melusine.eu.org/syracuse/immae/mp/physique-chimie/electromagnetisme/12.pdf
https://www.ipgp.fr/~grandin/Raphael_Grandin_personal_web_page/Teaching_files/3_EM.pdf
Calcul de la puissance par unité de surface (dans le cas d’un rayonnement isotrope)
Il s’agit de la surface d’une sphère qui est égale à 4pi.r2 (r étant le rayon de la sphère). Donc pour avoir la puissance rayonnée par unité de surface à la distance r, il suffit de diviser la puissance totale rayonnée par 4pi.r2.
Pour ceux que la physique ne rebute pas…
La puissance totale rayonnée est déterminée par le flux du vecteur de Poynting à travers une surface fermée. Le vecteur de Poynting, qui est un produit vectoriel des champs électriques et magnétiques, indique la densité de puissance rayonnée par unité de surface et par unité de temps. L’intégration de ce vecteur sur une surface fermée donne la puissance totale rayonnée par l’onde électromagnétique à travers cette surface.
En détail:
1. Le vecteur de Poynting :
Il est défini par la formule S = (E × H) / μ₀, où E est le champ électrique, H est le champ magnétique et μ₀ est la perméabilité du vide. Ce vecteur indique la direction et la magnitude de la densité de flux d’énergie, c’est-à-dire la puissance rayonnée par unité de surface.
2. Le flux du vecteur de Poynting :
Le flux est calculé en intégrant le vecteur de Poynting sur une surface. Mathématiquement, cela se traduit par l’intégrale du produit scalaire du vecteur de Poynting et du vecteur normal à la surface.
3. Puissance totale rayonnée :
Le flux du vecteur de Poynting à travers une surface fermée est égal à la puissance totale rayonnée par l’onde électromagnétique à travers cette surface. Cela signifie que la puissance rayonnée est égale à la quantité d’énergie qui traverse la surface par unité de temps.
4. Théorème de Poynting :
Le théorème de Poynting établit une relation entre la puissance rayonnée, la variation de l’énergie du champ électromagnétique et la puissance dissipée dans une distribution de charges.
5. Applications :
Le concept du vecteur de Poynting est essentiel dans la compréhension de la propagation des ondes électromagnétiques, ainsi que dans la conception d’antennes et d’autres dispositifs électroniques.
En résumé, le vecteur de Poynting est un outil crucial pour déterminer la puissance rayonnée par une onde électromagnétique. En calculant le flux de ce vecteur à travers une surface, on peut déterminer la quantité d’énergie qui traverse cette surface par unité de temps, ce qui correspond à la puissance rayonnée.
Il n’est pas indispensable de connaitre le contenu du texte précédent, en italique, pour comprendre l’aspect général de cet exposé.
Calcul du champ électrique d’une antenne isotrope (espace libre).
A l’aune de ce qui précède, et en appliquant la formule E2 = W x R, nous obtenons :
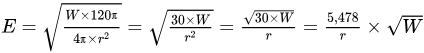
Le fameux 5
Dans laquelle W est la puissance fournie à l’antenne isotrope (rendement 100%).
Calcul du champ électrique d’un dipôle (espace libre).
Il suffit de multiplier le champ E calculé pour l’antenne isotrope par la racine carrée de la directivité du dipôle (la directivité s’exprime en rapport de puissances). Nous obtenons :

Dans laquelle 1,64 est la directivité et W est la puissance fournie au dipôle demi onde.
1,64 correspond à un gain de 2,15 dBi, en effet 10 x log (1.64) = 2.15
Rappel
Gain d’une antenne :
Une antenne isotrope n’a pas de gain, donc = 0 dB.
(C’est une antenne imaginaire qui rayonne uniformément dans toutes les directions).
Une antenne dipôle possède un gain de 2,15 dB par rapport à l’antenne isotrope. On dit aussi qu’elle a un gain de 2,15 dBi.
Le gain d’une antenne est exprimé plus généralement en dBd, c’est à dire par rapport au dipôle demi-onde.
En résumé:
gain en dBd = gain en dBi – 2,15 dB
gain en dBi = gain en dBd + 2,15 dB
Jean-Pierre Broillet, Microclub, mai 2025
